1、(1) 拉格朗日中值定理与柯西中值定理可以互相建立联系(可以抵消).
(2) 从形式上看:拉格朗日中值定理是 1 个 ;柯西中值定理是 2 个 . 那么
ξ的个数为 1 个,则用拉格朗日;
ξ的个数为 2 个(乘除),则用柯西.
若要求ξ^n互不相等,则需要分段。分段方式大致有两种:➀分段点可以抵消(需要构造分段点的值);➁分段点为ξ^n,则很可能是利用Cauchy中值定理反复求导来套娃
(3) 一把牛刀:Darboux定理

1


2

3


4

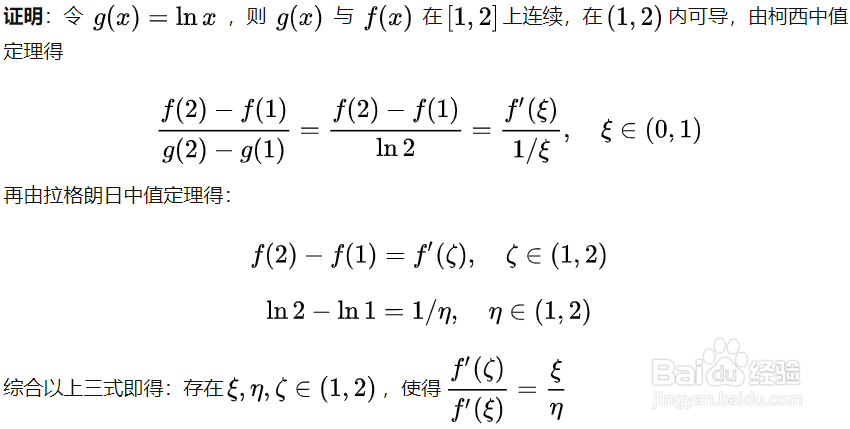
1

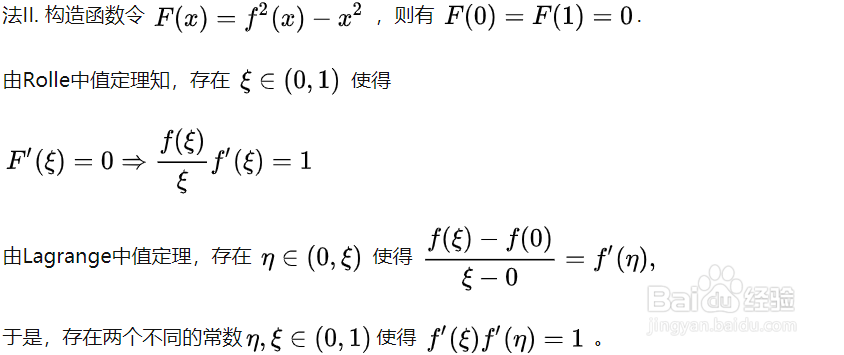

2

3


1


2


1、(1) 拉格朗日中值定理与柯西中值定理可以互相建立联系(可以抵消).
(2) 从形式上看:拉格朗日中值定理是 1 个 ;柯西中值定理是 2 个 . 那么
ξ的个数为 1 个,则用拉格朗日;
ξ的个数为 2 个(乘除),则用柯西.
若要求ξ^n互不相等,则需要分段。分段方式大致有两种:➀分段点可以抵消(需要构造分段点的值);➁分段点为ξ^n,则很可能是利用Cauchy中值定理反复求导来套娃
(3) 一把牛刀:Darboux定理

1


2

3


4

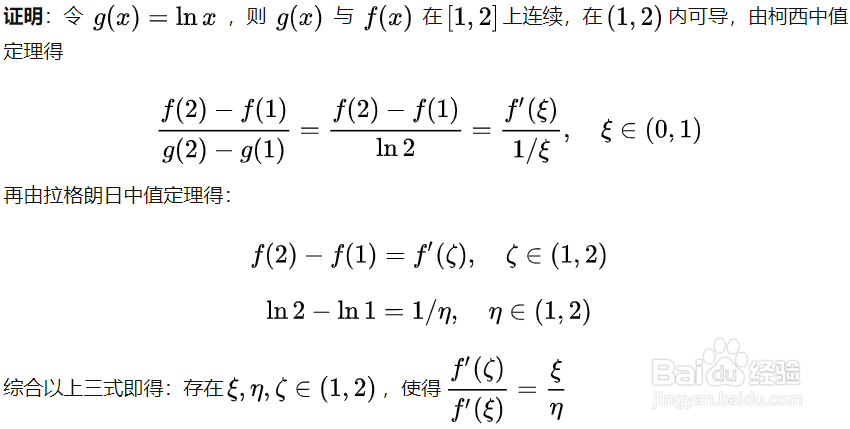
1

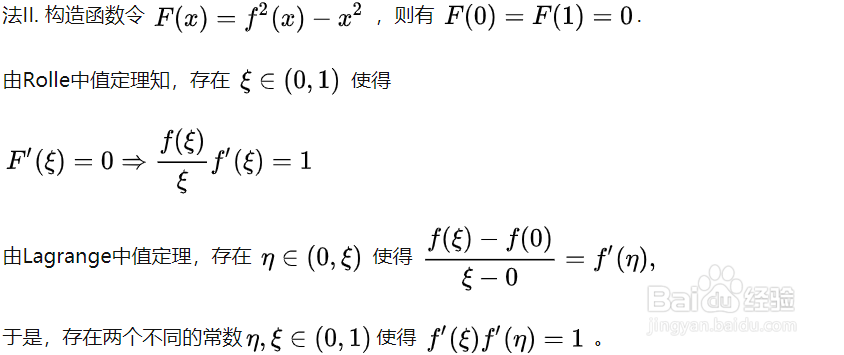

2

3


1


2

