1、在命令窗口,输入如下:
% Time interval
t = (1900:10:2000)';
% Population
p = [75.995 91.972 105.711 123.203 131.669 ...
150.697 179.323 203.212 226.505 249.633 281.422]';
% Plot
plot(t,p,'bo');
axis([1900 2020 0 400]);
title('Population of the U.S. 1900-2000');
ylabel('Millions');
按“Enter”键。
得如下图1所示。
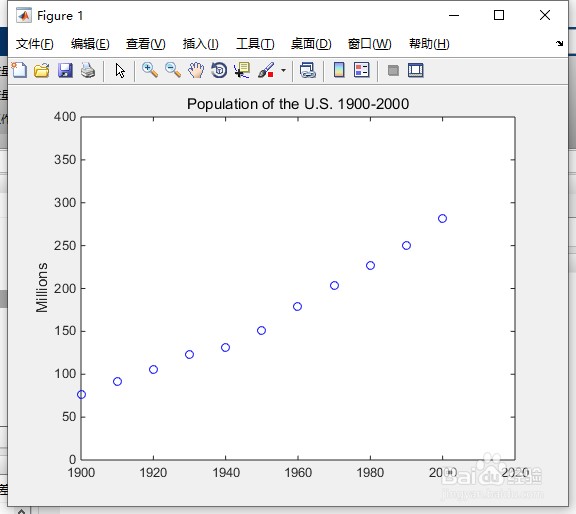
2、您对2010年的人口有何猜想?
输入如下命令:
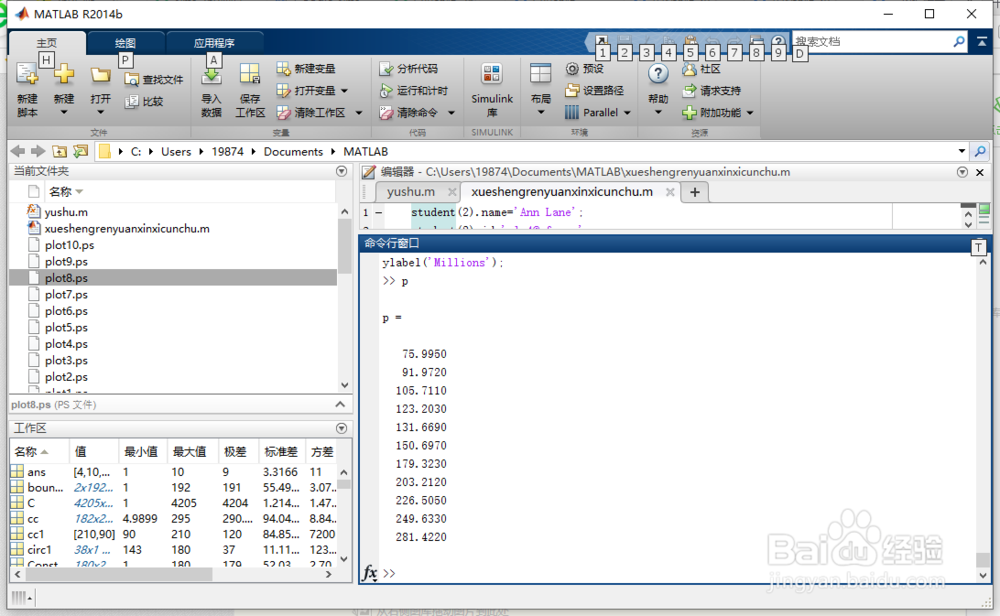
p
按“Enter”键。
得如下图2所示。
3、让我们用t中的多项式拟合数据并将其外推到t =2010。多项式中的系数是通过求解包含11 x 11 Vandermonde矩阵的线性方程组而获得的,该矩阵的元素是标度时间的幂 ,A(i,j)= s(i)^(nj);
程序如下:
n = length(t);
s = (t-1950)/50;
A = zeros(n);
A(:,end) = 1;
for j = n-1:-1:1
A(:,j) = s .* A(:,j+1);
end
拟合数据p的度为d的多项式的系数c是通过求解线性方程组而获得的,该线性方程组涉及Vandermonde矩阵的最后d + 1列: A(:,n-d:n)* c〜= p
4、如果d小于10,则方程式多于未知数,并且最小二乘法是合适的。 如果d等于10,则方程可以精确求解,并且多项式实际上是对数据进行插值的。 无论哪种情况,都可以使用MATLAB的反斜杠运算符来解决该系统。 这是三次拟合的系数。
输入如下程序:
c = A(:,n-3:n)\p
按“Enter”键。
得如图3所示。

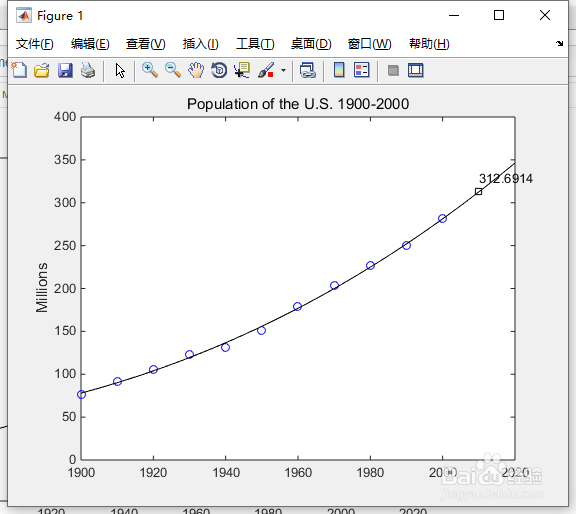
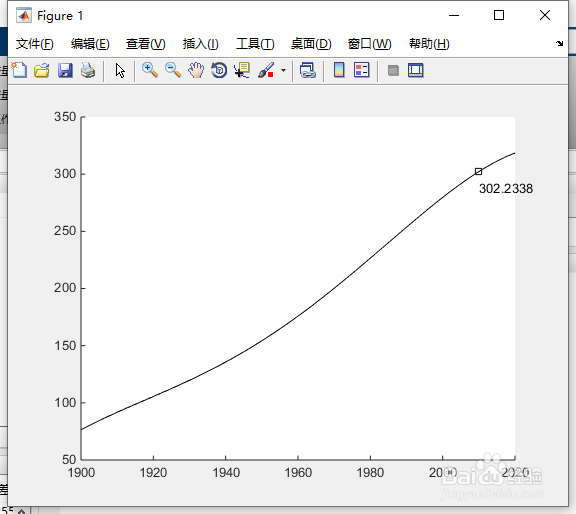
5、现在,我们评估1900年至2010年之间每年的多项式并绘制结果。
程序如下:
v = (1900:2020)';
x = (v-1950)/50;
w = (2010-1950)/50;
y = polyval(c,x);
z = polyval(c,w);
hold on
plot(v,y,'k-');
plot(2010,z,'ks');
text(2010,z+15,num2str(z));
hold off
按“Enter”键。
如图4所示。
6、比较三次拟合和四次拟合。 请注意,外推点非常不同。
程序如下:
c = A(:,n-4:n)\p;
y = polyval(c,x);
z = polyval(c,w);
hold on
plot(v,y,'k-');
plot(2010,z,'ks');
text(2010,z-15,num2str(z));
hold off
按“Enter”键。
如图5所示。
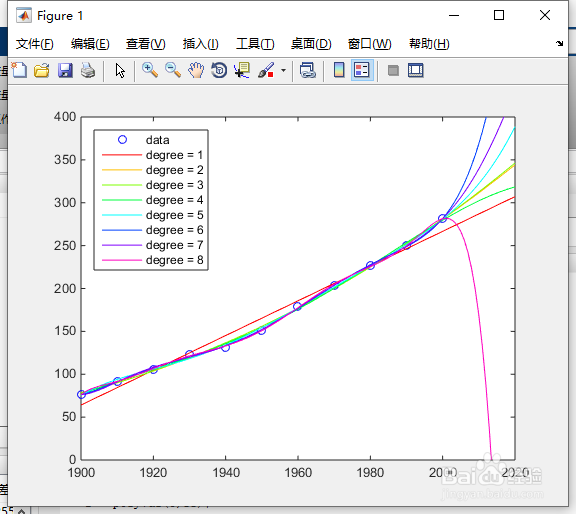
7、随着度数的增加,外推变得更加不稳定。
程序如下:
cla
plot(t,p,'bo')
hold on
axis([1900 2020 0 400])
colors = hsv(8);
labels = {'data'};
for d = 1:8
[Q,R] = qr(A(:,n-d:n));
R = R(1:d+1,:);
Q = Q(:,1:d+1);
c = R\(Q'*p); % Same as c = A(:,n-d:n)\p;
y = polyval(c,x);
z = polyval(c,11);
plot(v,y,'color',colors(d,:));
labels{end+1} = ['degree = ' int2str(d)];
end
legend(labels, 'Location', 'NorthWest')
hold off
按“Enter”键。
如图6所示。